matlab绘制MATLAB频域分析 奈氏图、根轨迹绘制
绘图简介
在复平面上表示传递函数的幅值相位角随频率的改变而改变的图就是nyquist图(奈奎斯特图,奈氏图),表示控制系统的幅相频率特性,横坐标U(real number)纵坐标jV(imaginary number);伯德图(bode)利用对数表示系统的幅频、相频特性,它分为两个图,一个是对数幅频图、一个是相频图,横坐标均为w,纵坐标一个为,一个为,,为相位角;而对数幅相图(nichols plot)则是将幅频和相频在一张图上表示出来了,横坐标是相位角fi(w)、纵坐标是增益K、然后图里面有不同的幅值线(幅值单位dB)。
这里的传递函数以惯性环节为例: 1/(Ts+1),T取0.01。
奈氏图
分子分母的系数分别存入两个1维矩阵,这里我利用了sys=tf()构造了系统sys。tf转换效果就是构造一些系统,比如你输入两个一维矩阵,那么就可以构造一个分式。具体见这里。nyquist(sys)直接把一个传递函数输入,然后绘出奈氏图[re,im,w]=nyquist(sys)则是根据需要返回传递函数将s替换成jw后的实部、虚部,还有相应的频率。
1 | num = [1]; %分子 |
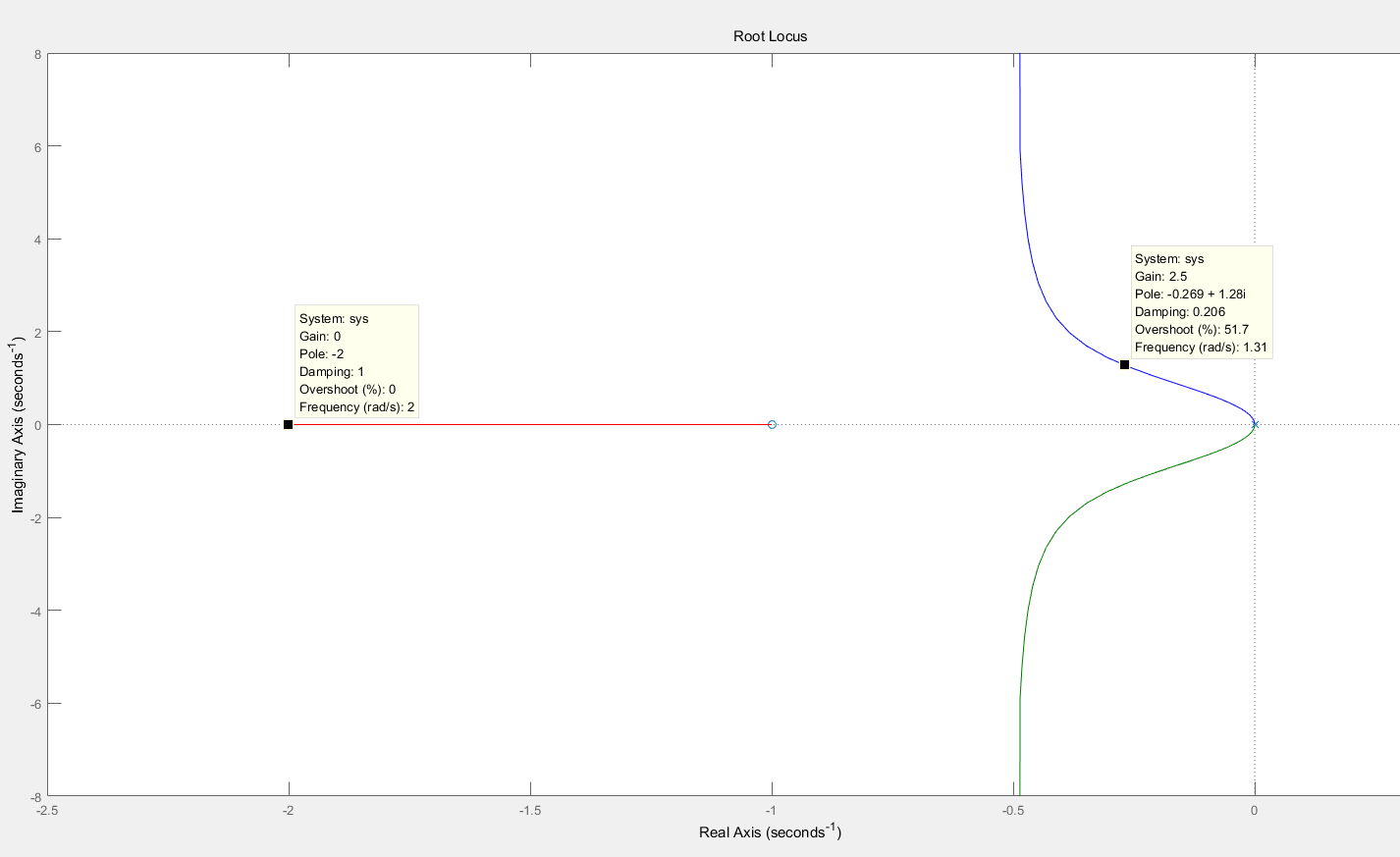
根轨迹图
以系统G(S)=K(s+1)/(s3+2s2)为例思路同上,对分子分母分别构造矩阵记为m,n
1 | m=[1 1] |
图中点的参数grain值就是K值
参考链接
不知道为啥这两个代码块总是渲染不好,不折腾了

Invitation
hgez6
666666
created:14/10/2022
Big Bird Luck Card
Be happy .
This is luck card,wish you a nice day .
评论